티스토리 뷰
이 포스팅은 차원 축소 기법 중 하나인 PCA에 대해 정리하는 글입니다.
개인적인 공부 내용을 남기는 글로 잘못된 점이 있다면 댓글로 알려주시면 감사하겠습니다.
1. Dimension of the greatest variability
PCA는 차원 축소 중 하나의 기법입니다. PCA를 알아보기 전 차원 축소의 접근 방법에 대해 먼저 생각해 보겠습니다. 시각적으로 이해하기 쉬운 2차원을 1차원으로 축소하는 예제를 같이 보시죠.
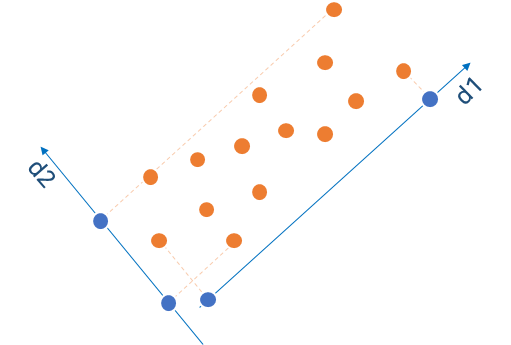
2차원의 데이터를 1차원으로 축소한다는 의미는 평면의 데이터를 선 하나로 표현한다는 의미와 같습니다. 위 그림에는 현재 2차원 데이터가 분포되어 있습니다. 이 데이터들을 1차원으로 옮기기 위해 먼저 데이터들을 가장 잘 표현하는 직선을 2개 찾았습니다. d1과 d2가 직선이 있습니다. 여러분은 두 개의 선들 중 어떤 선이 데이터들을 잘 표현할 수 있다고 생각하시나요?

데이터를 잘 표현하고 있다는 의미는 다른 데이터들과 거리가 충분히 떨어져 있다는 의미입니다. 위 그림에서 한번 이해해 보시죠. 데이터들을 d1으로 옮겼을 때와 d2로 옮겼을때 차이점이 보이시나요? 각각의 데이터들의 거리가 d2보다 충분하고 분류되는 개수도 많습니다.
이 처럼 각 데이터들 간의 거리가 충분하고 처음 데이터와 끝 데이터의 거리가 멀 수록 다양성이 높다고 할 수 있습니다. 다양성이라 함은 머신러닝에서는 Variance로 분산을 의미합니다. 차원을 축소를 접근할 때는 분산이 가장 높은 것을 선택해야 한다고 생각하고 접근해야 합니다.
2. PCA
PCA는 데이터의 분산(Variance)을 최대한 보존하면서 서로 직교하는 축을 찾아 고차원의 공간의 표본을 저 차원으로 변환하는 차원 축소 기법입니다. 위에서 본 내용으로 이해하자면 차원을 결정하는 성분 중 다양성을 최대한 보전하는 성분으로 변환하는 기법을 말합니다.

2가지 Feature가 있는 2차원을 예를 들어 보겠습니다. 데이터가 2차원에 놓여 있을 때 가장 분산이 잘 표현된 방향을 찾습니다. 그리고 그 방향을 1st Principal Component로 선택합니다. 다음으로 1st에 직교하는 축에 있는 2번째로 가장 크게 변하는 방향을 2nd Principal Component를 선택합니다.

주요 성분(Principal Component) 은 N개의 차원에서 N개의 주요 성분이 나오게 됩니다. 이렇게 나온 주요 성분 중 데이터들을 잘 표현하고 있는 주요 성분만 선택하여 사용합니다. 여기서 생각해야 할 것은 주요 성분은 기존에 있던 Feature의 값이 아닙니다. 기존의 Feature를 가지고 새롭게 정의된 성분이라는 것을 생각해야 합니다.
위 예제에서는 1stPC만 선택하여 성분을 옮겨 1차원으로 사용할 수 있습니다.
3. PCA 구하는 방법
1) 평균이 0이 되도록 데이터들을 노멀 라이즈 해줍니다.
현재 평균을 구해 각 데이터에 평균만큼 빼면 전체 평균이 0이 되도록 노멀 라이즈 할 수 있습니다.
$$ x_i = x_i - \mu $$
2) Covariance Matrix를 구합니다.
$$\sum = \left[\begin{array} {rr} cov(x_a, x_a) & cov(x_a, x_b) \\ cov(x_b, x_a) & cov(x_a, x_a) \end{array}\right] $$
3) EigenVector & EigenValue 를 구한다.
$$ \sum e = \lambda e $$
고유값(EigenValue)이 람다입니다. PCA에서는 이 고유값의 크기가 주요 성분의 중요도라고 할 수 있습니다. 이 성분의 크기가 가장 큰 것이 Variance이 높다 할 수 있고 고유 성분을 선택하는 기준이 됩니다.
해당 증명식은 다른 글을 참조하시면 좋을 것 같습니다.
4. PCA의 주요 성분 선택 방법
PCA에서 고유값을 구했다면 주요 성분을 선택하는 방법은 두가지 정도가 있습니다.
4-1 고유값을 퍼센트를 계산해 기준 값으로 주요 성분 선택하기
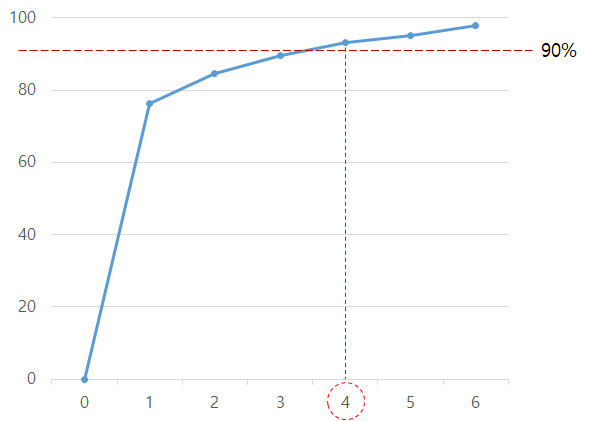
전체 고유 값을 %를 계산하여 선택 기준이 되는 threshold %를 정하고 기준을 넘는 부분까지 주요 성분을 선택합니다. 위 그래프는 90%를 기준으로 정하고 4개의 주요 성분을 선택하는 예제입니다.
4-2 고유값을 내림차순하여 주요 성분을 선택.

고유값 그대로 내림 차순으로 정렬하고 급격하게 완하 되는 지점으로 주요 성분의 개수를 선택합니다.
'머신러닝' 카테고리의 다른 글
| Wrapper Selection의 종류 - Forward & Backward Greedy, Genetic & Local Search (0) | 2020.02.22 |
|---|---|
| 차원 축소 - Feature Selection 3가지 방법 (0) | 2020.02.20 |
| [머신러닝] Dimensionality Reduction - 차원 축소 하는 이유? (0) | 2020.02.17 |
| 차원의 저주 - Curse of Dimensionality (0) | 2020.02.16 |
| SVM 서포트 백터 머신(Support Vector Machine) (0) | 2020.02.12 |
- Total
- Today
- Yesterday
- GPTGOT
- React 프로젝트 생성
- 버츄얼스튜디오코드
- GPT서비스
- k8s metrics-server
- numpy
- 파이썬
- git
- 퍼셉트론
- 에라토스테네스
- vscode
- 넘파이
- Python
- react
- 파이썬 numpy
- Java
- LeetCode 풀이
- Component
- 머신러닝
- Node
- Java leetcode
- LeetCode 5월 챌린지
- 지도학습
- 리엑트
- 노드
- k8s metrics-server running
- LeetCode 알고리즘 공부
- LeetCode 30일 챌린지
- CHATGOT
- 30 Day LeetCode Challenge
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
