티스토리 뷰
차원의 저주 - Curse of Dimensionality에 대해 정리해보겠습니다.
1. 차원의 저주
일상적으로 경험하는 3차원 물리 공간에서 발생하지 않는 현상으로 고차원 데이터를 분석하거나 구성하는 과정에서 발생하는 다양한 현상을 말합니다. 머신러닝에서 많은 Feature를 가지고 있다는 것은 고차원 공간의 Data를 다루고 있다는 의미로 차원의 저주에 대해 생각하고 있어야 합니다.
2. 차원의 저주 현상
2-1 데이터의 밀집도 (Data Density)

차원이 다르면 Data의 밀집도가 달라집니다.
위 그림은 N개의 Data를 서로 다른 차원에서 다룰때 데이터의 밀집도가 달라지는 모습을 표현하고 있습니다.
- 1차원에서 데이터의 밀집도는 N/5로 하나의 큐브는 N/5 샘플을 가지게 됩니다.
- 2차원에서 데이터의 밀집도는 N/25로 하나의 큐브는 N/25 샘플을 가지게 됩니다.
- 3차원에서 데이터의 밀집도는 N/125로 하나의 큐브는 N/125 샘플을 가지게 됩니다.
차원이 높아 지면 데이터의 밀집도는 작아지는 것을 볼 수 있습니다.
2-2 Geometric Insanity
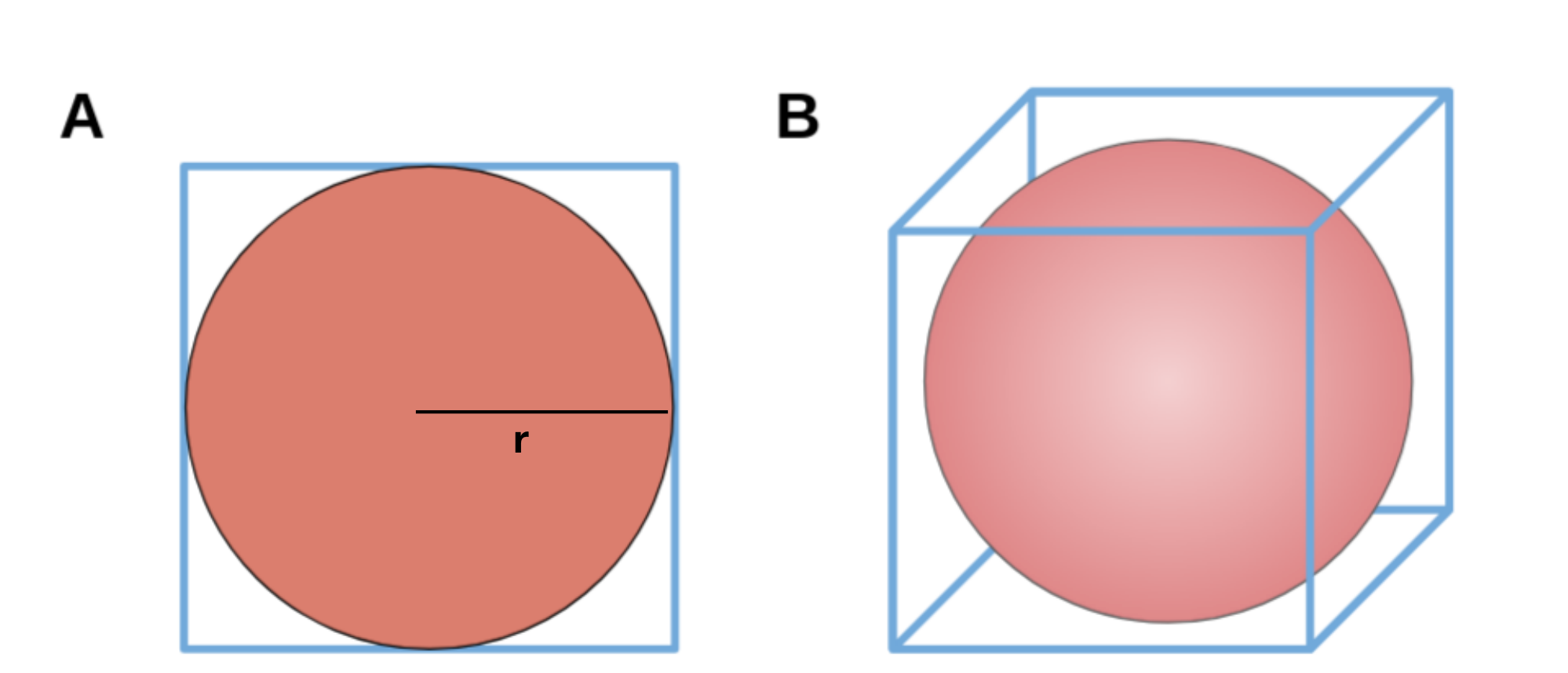
차원이 높아짐에 따란 어떠한 한 점이 나타내는 영역이 작아진 다는 의미를 확인할 수 있는 부분이 Geometric Insantiy입니다. 위 그림은 2차원, 3차원에서의 구가 나타내는 영역을 표현하고 있습니다.
2차원 영역 및 구의 크기 비율
$$ Square Area : (2r)^2 $$
$$ Circle Area : \pi r^2$$
$$ Circle / Square ≒ 78.5 % $$
3차원 영역 및 구의 크기 비율
$$ Cube Vol: (2r)^3 $$
$$ Sphere Vol : 4 \pi r^3 /3 $$
$$ Circle / Square ≒ 52.4% $$
2차원과 3차원을 비교했을 때 영역의 크기는 78.5% -> 52.4%로 줄어들게 됩니다. 3차원에서 4차원으로 변할 때도 점점 구의 크기가 작아지게 되는데 차원과 크기를 2차원 차트로 표현하면 아래와 같습니다.

차원이 높아지면서 점점 해당 영역이 작아지게 됩니다. 여러 점들이 작은 차원에 있다가 고차원으로 가게 되면 점들은 점점 외각(corner)으로 이동하게 되고 각 점들의 거리는 멀어지게 됩니다.
3. 차원의 저주를 탈출하기 위한 방법
차원이 높아지면 데이터의 밀집도가 증가하며 모든 것이 작아지고 부족하게 됩니다. 차원의 저주를 해결하기 위ㅙ 차원을 줄이는 기법들이 머신러닝에서 사용되고 있습니다.
다음은 차원을 줄이는 방법 리스트입니다. 자세한 설명은 참고 문헌을 참고 부탁드립니다.
- Multidimensional Scaling (MDS)

- Principal Components Analysis (PCA)
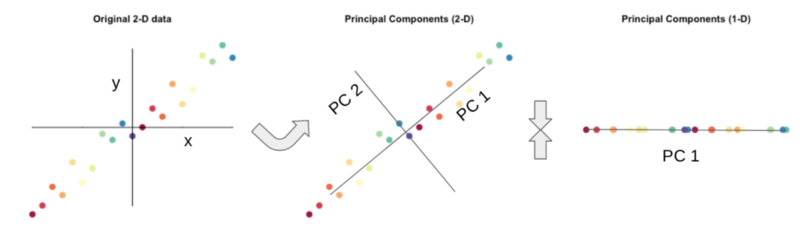
- Linear Discriminant Analysis (LDA)
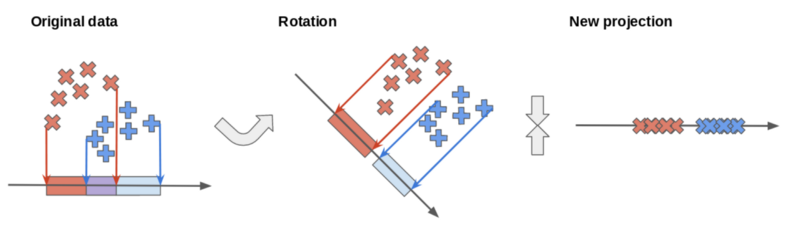
- lsomap

- Laplacian Eigenmapping
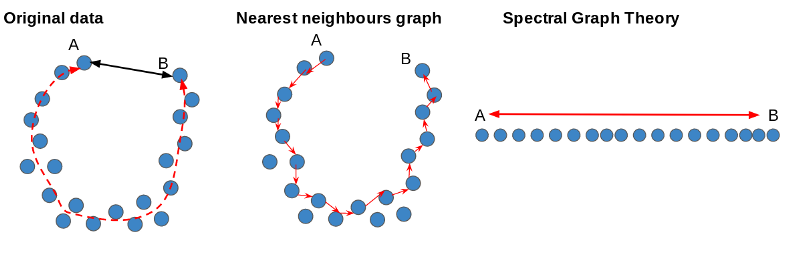
사진 및 문헌 참고
'머신러닝' 카테고리의 다른 글
| 차원축소 - PCA (Principal Component Analysis) (0) | 2020.02.19 |
|---|---|
| [머신러닝] Dimensionality Reduction - 차원 축소 하는 이유? (0) | 2020.02.17 |
| SVM 서포트 백터 머신(Support Vector Machine) (0) | 2020.02.12 |
| KNN(K-Nearest Neighbor) 알고리즘 - Python 예제 (1) | 2020.02.01 |
| 머신러닝의 종류 - 비지도(Unsupervised )학습, 지도(Supervised )학습 (0) | 2020.01.31 |
- Total
- Today
- Yesterday
- 파이썬 numpy
- Node
- 넘파이
- Java leetcode
- 노드
- vscode
- 지도학습
- Java
- k8s metrics-server running
- 30 Day LeetCode Challenge
- LeetCode 알고리즘 공부
- Python
- 버츄얼스튜디오코드
- GPTGOT
- 퍼셉트론
- react
- 에라토스테네스
- React 프로젝트 생성
- numpy
- git
- LeetCode 30일 챌린지
- CHATGOT
- GPT서비스
- k8s metrics-server
- LeetCode 풀이
- 머신러닝
- 파이썬
- Component
- LeetCode 5월 챌린지
- 리엑트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
